الشيء العظيم في الهندسة هو أنه يمكنك اثباتها باستخدام الصور والأشكال. من الأمثلة على ذلك، مبرهنة فيثاغورس الشهيرة عن المثلث القائم. سنكتب |أ| و |ب| للضلعين الصغيرين و|جـ| للضلع المواجه للزاوية القائمة (الوتر).
فنجد أن: جـ2 = أ2 + بـ2
(a²+b²=c²)
الشكل التالي يوضح ثلاثة براهين بصرية لمبرهنة فيثاغورس. الإثبات البصري الأول هو في الغالب الذي استخدمه فيثاغورس نفسه ليثبت نظريته.
الإثبات البصري الثاني مشابه للذي استخدمه عالم الرياضيات الهندي القديم «بهاسكارا – Bhaskara».
أما الإثبات البصري الثالث فيعود في الأصل للرئيس الـ 20 للولايات المتحدة، «جيمس غارفيلد – James Garfield». وبالمناسبة، نحن نتساءل ما إذا كان الرئيس الأمريكي الحالي يشغل نفسه بالهندسة في وقت فراغه أم لا.
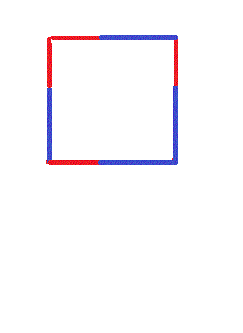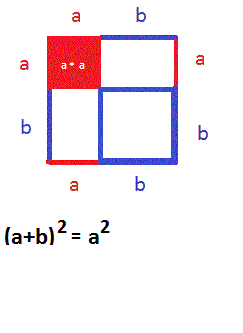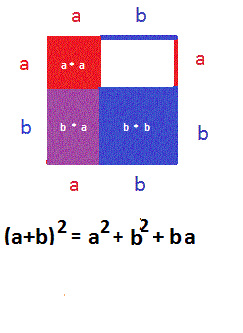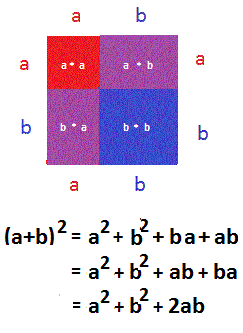
يُلاحظ أن الإثبات بصري أعلاه يستخدم المعادلة التالية:
(أ +بـ)2 = أ2+2 أ بـ +بـ2
[²=a²+2ab+b²(a+b)]
وهذا أيضًا يمكن إثباته باستخدام الصور.
- ترجمة: مصطفى العدوي
- تدقيق: المهدي الماكي
- تحرير: أحمد عزب
- المصدر
