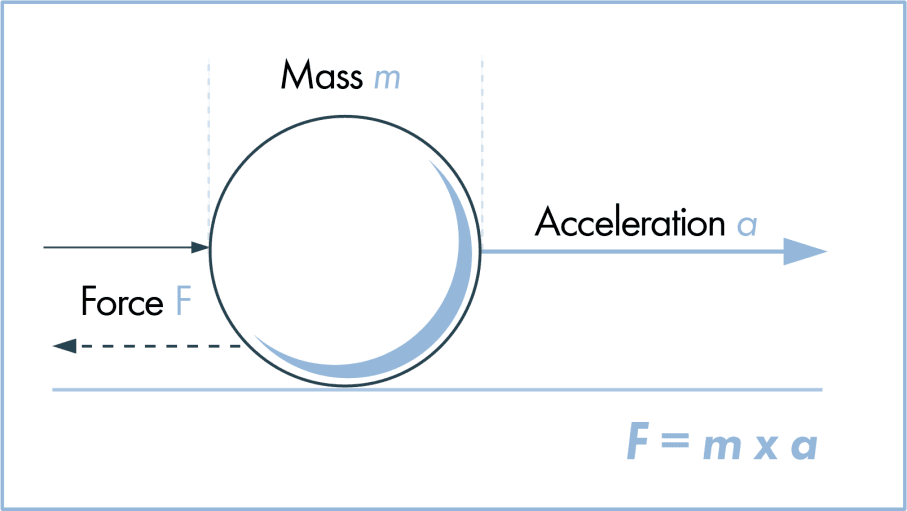
ينص قانون نيوتن الأول للحركة على أن الجسم الساكن يبقى ساكنًا والجسم المتحرك يبقى متحركًا ما لم تؤثر عليه قوة خارجية. إذن ما الذي يحدث للجسم عندما تؤثر عليه قوة خارجية؟ يوصف هذا الموقف في قانون نيوتن الثاني للحركة. وفقًا لوكالة ناسا، ينص هذا القانون على أن القوة تساوي التغيُّر في الزخم لكل تغيير في الزمن. بالنسبة للكتلة الثابتة، فإن القوة تساوي الكتلة في التعجيل. وهذا يكتب على الشكل الرياضي F = ma.
حيث F هي القوة، m تمثل الكتلة وa هي التعجيل. الرياضيات وراء ذلك بسيطة جدًا. إذا قمت بمضاعفة القوة، فإنك تضاعف التعجيل، ولكن إذا قمت بمضاعفة الكتلة، فإنك تقلل التعجيل إلى النصف.
نشر نيوتن قوانين الحركة الخاصة به في عام 1687، في كتابه "Philosophiæ Naturalis Principia Mathematica" (المبادئ الرياضية للفلسفة الطبيعية)، حيث صاغ الوصف لكيفية تحرك الأجسام تحت تأثير القوى الخارجية.
توسَّع نيوتن في الأعمال السابقة لجاليليو غاليلي، الذي طوَّر أول قوانين دقيقة لحركة الأجسام، وفقًا لكريك بوثن Greg Bothun، أستاذ الفيزياء بجامعة أوريغون، أظهرت تجارب جاليليو أن جميع الأجسام تتسارع بنفس المعدل بغض النظر عن الحجم أو الكتلة.
كما توسع نيوتن وعقَّب على أعمال رينيه ديكارت Rene Descartes الذي نشر أيضًا مجموعة من قوانين الطبيعة في عام 1644 أي بعد عامين من ولادة نيوتن. قوانين ديكارت مشابهة جدًا لقانون نيوتن الأول للحركة.
التعجيل والسرعة
ينص قانون نيوتن الثاني للحركة على أنه عندما تؤثر قوة ثابتة على جسم ذو كتلة فإنها تتسبب في تسارعه، أي تتغير سرعته بمعدل ثابت. في أبسط الحالات، تؤدي القوة المطبقة على جسم في حالة سكون إلى تعجيله باتجاه القوة.
ومع ذلك إذا كان الجسم متحركًا بالفعل أو إذا عرض هذا الموقف من خلال إطار مرجعي قصوري متحرك، قد يظهر أن هذا الجسم يتسارع أو يتباطأ أو يغير اتجاهه اعتمادًا على اتجاه القوة والاتجاهات التي يتحرك بها الجسم والإطار المرجعي بالنسبة لبعضهما البعض.
تشير الأحرف F و a في المعادلة؛ إلى أن القوة والتعجيل عبارة عن كميات متجهة، ما يعني أن لكل منهما مقدارًا واتجاهًا. يمكن أن تكون القوة عبارة عن قوة واحدة أو يمكن أن تكون مزيجًا من عدة قوى. في هذه الحالة، تكتب المعادلة كـ F = ma∑.
يمثل الحرف الكبير Σ (الحرف اليوناني سيجما) المحصلة الاتجاهية لجميع القوى أو القوة الصافية التي تؤثر على جسم ما.
من الصعب أن نتخيل تطبيق قوة ثابتة على جسم لفترة زمنية غير محددة. في معظم الحالات لا يمكن تطبيق القوى إلا لفترة محدودة، ما ينتج عنه ما يسمى بالدافع أو الاندفاع.
بالنسبة للجسم الذي يتحرك في إطار مرجعي بالقصور الذاتي دون تأثير أي قوى أخرى مثل الاحتكاك الذي يؤثر عليه، فإن دافعًا معينًا سيتسبب في حدوث تغيير معين في سرعته. قد يسرع الجسم أو يبطئ أو يغير اتجاهه وبعد ذلك سيستمر الجسم في التحرك بسرعة ثابتة جديدة (إلا إذا تسبب الدافع في إيقاف الجسم).
ومع ذلك هناك حالة واحدة نواجه فيها قوة ثابتة؛ القوة الناتجة عن تعجيل الجاذبية، والتي تسبب بذل الجسم لقوة هابطة على الأرض. في هذه الحالة، يتم كتابة التعجيل المستمر بسبب الجاذبية g، ويصبح قانون نيوتن الثاني؛ F = mg. نلاحظ أنه في هذه الحالة، لا يتم كتابة F و g بشكل تقليدي على أنهما متجهات، لأنهما يشيران دائمًا في نفس الاتجاه، للأسفل.
يُعرف ناتج ضرب الكتلة في التعجيل الأرضي mg بالوزن، وهو نوع آخر من القوة. دون الجاذبية، ليس للجسم ذو الكتلة أي وزن، ودون الجسم ذو الكتلة، لا يمكن للجاذبية أن تنتج قوة. من أجل التغلب على الجاذبية ورفع الجسم، يجب أن تنتج قوة تصاعدية ma أكبر من قوة الجاذبية النزولية mg.
قانون نيوتن الثاني للحركة على أرض الواقع
تتبع الصواريخ التي تسافر في الفضاء جميع قوانين نيوتن الثلاثة للحركة، إذا احتاج الصاروخ إلى إبطاء حركته أو تسريعها أو تغيير اتجاهه تستخدم القوة لإعطائه دفعة، وتأتي عادةً من المحرك. مقدار القوة والموقع الذي توفرت فيه الدفعة يمكن أن يغير إما السرعة (القيمة الكمية للتعجيل) أو الاتجاه أو كليهما.
والآن بعد أن علمنا كيف يتصرف جسم ذو كتلة في إطار مرجعي بالقصور الذاتي عند تعرضه لقوة خارجية، مثل كيفية قيام المحركات بإنشاء دفعة المناورة بالصاروخ؛ ما الذي يحدث للجسم الذي يبذل تلك القوة؟ توصف هذه الحالة في قانون نيوتن الثالث للحركة.
الهوامش:
*الإطار المرجعي القصوري (Inertial Reference Frame): هو عبارة عن نظام إحداثيات يعرف بكونه ذو حركة قصورية (أي مختبر فيزيائي ساكن أو يتحرك حركة منتظمة وفي خط مستقيم بالنسبة لنا، ويسود فيه القصور الذاتي). وهذا ما يميزه عن الإطار المرجعي اللا قصوري (المختبر الذي يتحرك حركة متسارعة، أو في حركة دائرية).
* الاندفاع (Impulse) في الفيزياء ورمزه (J أو I) وهو وفقًا لتعريفه الاصطلاحي تكامل القوة بالنسبة للزمن ووحدة قياسه (نيوتن.ثانية N.s).
اقرأ ايضًا:
ترجمة: سرمد يحيى
تدقيق: محمد نجيب العباسي
الكاتب
سرمد يحيى