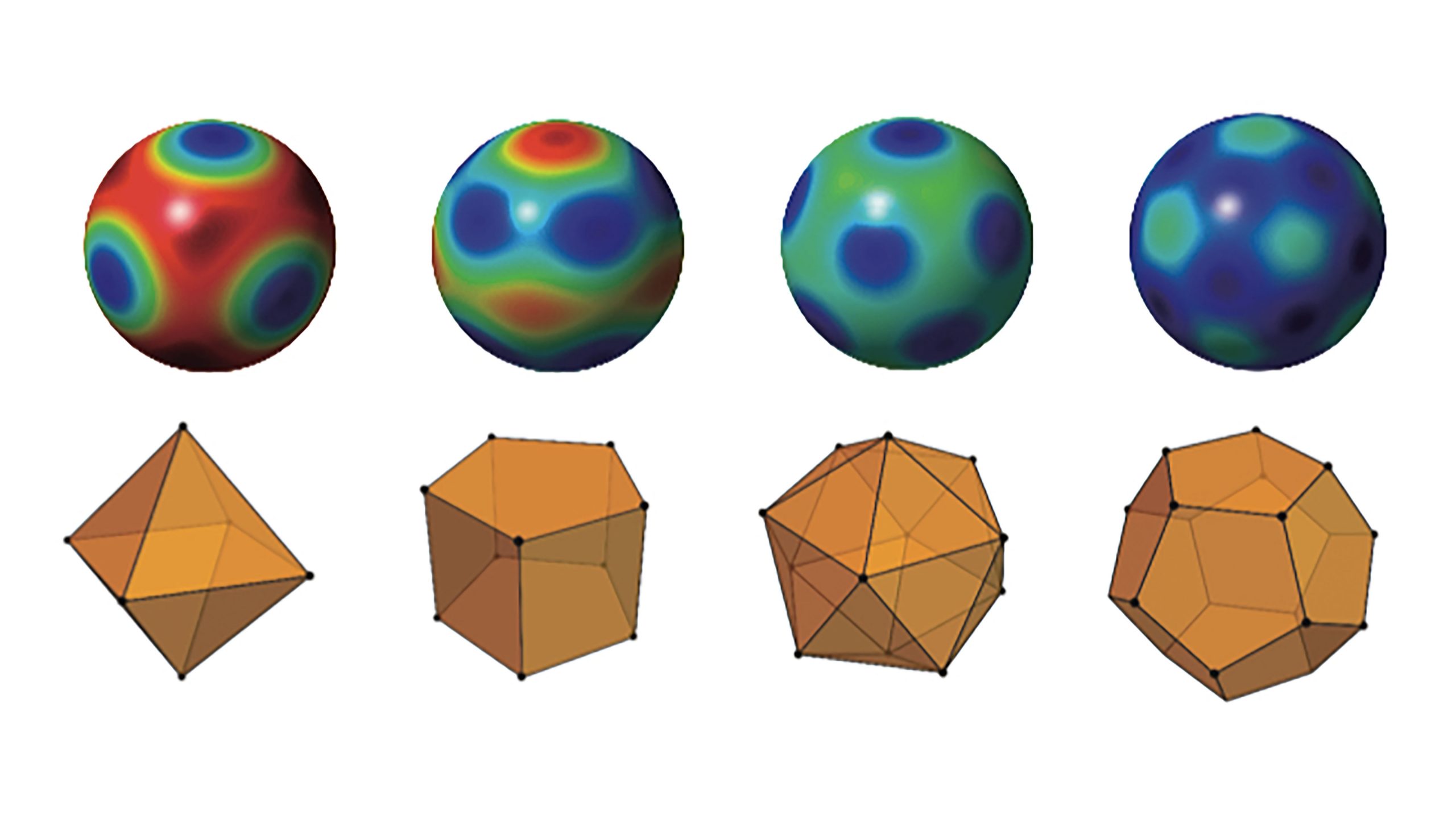هل يُعد جزيء الضوء «الفوتون» كرةً صغيرة تتحرك عبر الفضاء، أم أنه كيان فوضوي موجود في كل مكان في نفس الوقت؟ يعتمد الجواب على: هل ننظر وفقًا لقوانين الجزيئات تحت الذرية (ميكانيكا الكم)، أم للمعادلات الحتمية التي تحكم الأجسام الكبيرة (النسبية)؟
في سابقة من نوعها، وجد الفيزيائيون طريقة رياضية لتحديد درجة الكم لأي شيء -جسيم أو ذرة أو جزيء أو كوكب- فهي تحدد كمومية الأشياء «وأكثر الحالات كمومية لنظام ما»، التي يسميها العلماء: «ملوك الحالة الكمومية وملكاتها».
إضافة إلى تعزيز فهمنا للكون، قد يكون لهذا الاكتشاف تطبيقات عملية في التكنولوجيا الكمية، مثل كاشفات موجات الجاذبية وأجهزة القياس فائقة الدقة.
في الواقع تحت الذري، يسود العالم الغريب لميكانيكا الكم. وتبعًا لقواعده التي تتحدى المنطق البشري، قد تنخرط الجسيمات دون الذرية الصغيرة مثل الإلكترونات في حالات فائقة غريبة، ما يعني أن الإلكترون قد يوجد في حالات متعددة في آنٍ واحد، ولا يثبت موقعه حول الذرة أو عزمه حتى يُلاحظا بأجهزة القياس، حتى أن هذه الجسيمات الصغيرة لديها القدرة على اختراق حواجز لا يمكن التغلب عليها نظريًّا.
تتبع الأشياء التي نراها في حياتنا اليومية الفيزياء الكلاسيكية، مثلًا، تتدافع كرات البلياردو معًا، وتطير قذائف المدفعية على امتداد أقواس مكافئة، وتدور الكواكب في مداراتها وفقًا لمعادلات فيزيائية معروفة.
فكر الباحثون منذ فترة طويلة في هذه الحالة الغريبة، فوجدوا أنه يمكن تعريف بعض الموجودات في الكون بطريقة كلاسيكية، في حين تخضع غيرها لقوانين الكم الاحتمالية، ما يعني إمكانية قياس نتائجها المحتملة فقط.
وفقًا لميكانيكا الكم، فإن «كل شيء يخضع لميكانيكا الكم». قال آرون غولدبيرغ، الفيزيائي في جامعة تورنتو في كندا، المؤلف الرئيس للورقة البحثية الجديدة: «إذا كنت لا ترى هذه الأشياء الغريبة كل يوم، فهذا لا يعني أنها غير موجودة».
ما يعنيه غولدبيرغ أن الأجسام الكلاسيكية -مثل كرات البلياردو- هي أنظمة كمومية سرًّا، أي إنه توجد احتمالية محدودة جدًا أن تخترق -مثلًا- جانب طاولة البلياردو، ويشير ذلك إلى وجود علاقة تبادلية بين الفيزياء الكلاسيكية من جهة والكم من جهة أخرى.
قبل فترة وجيزة، كان أحد المؤلفين المشاركين لغولدبيرغ -لويس سانشيز سوتو من جامعة كومبلوتنسي في مدريد- يلقي محاضرة، عندما سأله أحد المشاركين: «ما الحالة الأكثر كمومية التي قد تسود نظامًا ما؟»، يقول سانشيز سوتو: «هذا السؤال هو ما دفعنا إلى البحث».
كانت المحاولات السابقة لتحديد الكم تُجرى ضمن أنظمة كمومية معينة -مثل المحتوية على جزيئات الضوء- ومن ثم، لا يمكن بالضرورة تطبيق النتائج على أنظمة أخرى تتضمن جسيمات مختلفة مثل الذرات، وبدلًا من ذلك، بحث غولدبيرغ وسانشيز سوتو وفريقهما عن طريقة عامة لتحديد أكثر الحالات الكمومية تطرفًا.
قال غولدبيرغ: «يمكننا تطبيق هذا على أي نظام كمي، مثل الذرات أو الجزيئات أو الضوء أو حتى مزيج من هذه الأشياء، باستخدام نفس المبادئ التوجيهية»، وجد الفريق أن لهذه الظواهر الكمومية المتطرفة نوعين مختلفين على الأقل. وسمّوا الأولى «ملوكًا» والثانية «ملكات» تعبيرًا عن طبيعتها الفائقة المتطرفة.
ما الذي يعنيه بالضبط أن يكون الشيء «أكثر كمومية»؟ سيكون الشرح انطلاقًا من هذا المفهوم صعبًا، لأنه رياضي معقد ويصعب تخيله بسهولة.
اقترح الفيزيائي في جامعة شفيلد، غير المشارك في البحث بيتر كوك طريقةً لفهمها إذ قال: «أحد أبسط الأنظمة الفيزيائية هو النواس التوافقي البسيط، أي كرة في نهاية نابض تتحرك ذهابًا وإيابًا».
يكون الجسيم الكمي عند أقصى حدوده الفيزيائية الكلاسيكية إذا تصرف مثل الكرة الموجودة في نظام النواس النابض، بمعنى أنه موجود في نقاط معينة محددة زمنيًّا بناءً على الدفع الأولي الذي تعرّض له. ولكن، إذا بُعثر الجسيم في المستوى الميكانيكي الكمي بطريقة تجعله بلا موقع محدد في الفضاء، ثم عُثر عليه في مسار النابض والكرة، فهذا يعني أنه في إحدى هذه الحالات الكمومية القصوى.
رغم خصوصيتها، يعدّ بيتر كوك هذه النتائج مفيدة للغاية ويأمل أن يكون لها تطبيق واسع النطاق. قال: «إن معرفة وجود حد أساسي يتصرف عنده النظام بأكبر قدر ممكن من الكمومية تشبه معرفة أن سرعة الضوء موجودة. إن هذا الاكتشاف يضع قيودًا على الأشياء التي يصعب تحليلها».
قال غولدبيرغ إن التطبيقات الأكثر وضوحًا وبدهية لهذا الاكتشاف هي في مجال علم القياس الكمي، وفيه يحاول المهندسون قياس الثوابت الفيزيائية وغيرها من الخصائص بدقة متناهية. مثلًا، يجب أن تكون أجهزة الكشف عن موجات الجاذبية قادرة على قياس المسافة بين مرآتين بنسبة أفضل من 1/10000 من حجم نواة الذرة. وباستخدام المبادئ التي اكتشفها الفريق، قد يتمكن الفيزيائيون من تحسين هذا العمل الرائع.
قد تساعد النتائج الباحثين أيضًا في مجالات مثل اتصالات الألياف الضوئية ومعالجة المعلومات والحوسبة الكمومية. قال غولدبيرغ بحماس: «يُحتمل أنه يوجد العديد من التطبيقات التي لم نفكر فيها».
اقرأ أيضًا:
مفارقة كمية جديدة تضع أسس الواقع المرصود موضع تساؤل
خوارزمية ذكاء اصطناعي يمكنها تعلم قوانين ميكانيكا الكم!
التناظر الفائق.. الطريقة المثالية لدمج ميكانيكا الكم بالجاذبية
ترجمة: أناغيم أبو خضور
تدقيق: علي البيش
مراجعة: أكرم محيي الدين
الكاتب
أناغيم أبو خضور