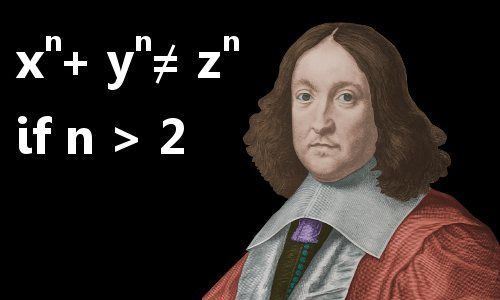يُعتبر (بيير دي فيرما – Pierre de Fermat) واحدًا من أعظم علماء الرياضيات في التاريخ، ويُعتبر -هو و(رينية ديكارت – René Descartes)- من أبرز علماء الرياضيات في النصف الأوّل من القرن السابع عشر.

قدّم بيير دي فيرما مساهمات كبيرة جدًّا في ميادين واسعة من الرياضيات، فهو يُعرف بمؤسّس نظرية الأرقام المعاصرة، وكان مُرشدًا في اختراع حساب التفاضل والتكامل، فأساليبه لإيجاد الظلّ أو الميل (tangent) للمنحنيات وحدودها القصوى والدنيا جعلته يُعتبر مخترعًا لحساب التفاضل.

بيير دي فيرما عالم رياضيات فرنسي وُلد في 17/آب/1601 في (بيمون دي لوماين، فرنسا – Beaumont-de-Lomagne, France) وتوفي في 12/كانون الثاني/1665 في (كاستر –Castres).

تلقّى دي فيرما تعليمه الأساسي في مدرسة فرنسية محليّة، وفيما بعد درس القانون وتخرّج عام 1631 بشهادة بكالوريوس الحقوق من (جامعة أورلينز – University of Orléans)، وأصبح مستشارًا عام 1634، ثُمَّ عُيّن في محكمة الجرائم عام 1638 لكنّه كان مهتمًّا باللّغات الأجنبيّة، والأدب الكلاسيكي، والعلوم القديمة، وبالطبع الرياضيات.

دراسة دي فيرما للمنحنيات والمعادلات دفعته لتعميم معادلة القطع المكافئ العادي ay = x^2، ومعادلة القطع الزائد المتعامد = a^2 ، إلى الشكل a^(n-1)y=x^n، وتُعرَف المنحنيات التي تحدّدها هذه المعادلة بأنّها القطوع المكافئة والزائدة لفيرما، باعتبار n قيمة موجبة أو سالبة.

وبالمثل عمّم فيرما معادلة أرخميدس للقوس الحلزوني r = aθ ، وهذه المنحنيات بدورها وجّهته في منتصف 1630 إلى خوارزمية -أو قاعدة لعمليّة رياضية- مكافئة للتفاضل.

مكنّه هذا الإجراء من العثور على معادلات لميل المنحنيات، وتحديد أماكن الحد الأقصى والحد الأدنى، ونقاط انعطاف المنحنيات متعدّدة الحدود، والتي تمثّل رسومًا بيانية للمجموعات الخطيّة من قوى المتغيّر المستقل.

خلال نفس السنوات، وجد صيغًا للمناطق التي تحدّها هذه المنحنيات من خلال عملية تجميع تُكافئ المعادلة المستخدمة الآن للغرض نفسه في حساب التفاضل والتكامل.

وقد كتب إسحاق نيوتن أنّ أفكاره المبكّرة حول حساب التفاضل والتكامل جاءت مباشرة من (طريقة فيرما في رسم الظلال -Fermat’s way of drawing tangents).

شارك دي فيرما بشكل مستقلّ في ابتكار الهندسة التحليلية باكتشافه المبدأ الأساسي لها، واخترع نظرية الاحتمالات بالتعاون مع (بليز باسكال – (Blaise Pascal.

أجرى أبحاثًا عن وزن الكرة الأرضيّة، وانكسار الضوء، والبصريّات، وقدّم مساهمات بارعة في نظرية الأعداد، ومنها نظريّته الأخيرة الموضّحة في الصورة أعلاه، فهي الدليل الذي ظلَّ يتحدّى جهود أفضل علماء الرياضيات لأكثر من ثلاثة قرون.

وتفيد تلك النظريّة بأنّه لا يمكن تقسيم عدد مرفوع لأسّ إلى مجموع عددين مرفوعين لنفس الأسّ.

وإليكم أشهر أقواله:

  •  «من المستحيل لأيّ رقم مرفوع لأسّ أكبر من 2 أن يُكتَب كمجموع رقمين مرفوعين لنفس الأسّ. لديَّ إثبات عجيب حقًا لهذا الاقتراح ولكنَّ هذه الزاوية ضيّقة جدًّا لاحتواء ذلك الإثبات».
  •  «أنا أكثر استثناءً واختلافًا عن أي رجلٍ في العالم».
  •  «وربّما ستشكرني الأجيال القادمة لأنّني أظهرتُ أنّ القدماء لم يعلموا كلّ شيء».
  •  «سأشاركك كلّ هذا كلّما رغبت في ذلك».
  •  «لقد وجدتُ عددًا هائلًا من النظريّات مفرطة الجمال».
  •  «من المستحيل تقسيم عدد مرفوع للأسّ 3 إلى مجموع عددين مرفوعين للأسّ 3، أو تقسيم عدد مرفوع للأسّ 4 إلى مجموع عددين مرفوعين لنفس الأسّ، أو بشكل عام تقسيم أيّ عدد مرفوع لأيّ أسّ ما عدا 2 إلى مجموع عددين مرفوعين لنفس الأسّ، وقد وجدتُ إثباتًا ملحوظًا لهذا، ولكنّ هذا الهامش ضيّق جدًا ولا يمكنه احتوائه».