مسلمات إقليدس
إقليدس السكندري (Euclid of Alexandria) رياضي إغريقي عاش منذ أكثر من 2000 عام مضت، وكثيرًا ما يُطلق عليه لقب أبو الهندسة. يعد كتابه “الأصول” – “The Elements” أحد أكثر الكتب نجاحًا في التاريخ، ويقول البعض أن الكتاب المقدس هو الكتاب الوحيد الذي نُشر أكثر منه. يُعد ذلك الكتاب أيضًا أول طرح نظامي عن الهندسة. وضع فيه إقليدس قواعد الهندسة.
كان إقليدس مهتمًا بجميع الأشياء التي يمكن فعلها باستخدام حافة مستقيمة (مسطرة بدون ترقيم) وبوصلة.
ووضع مجموعته الخاصة من خمس قوانين تصف بعض الأشياء البسيطة التي يمكن فعلها بتلك الأدوات، بالإضافة إلى بعض الحقائق حول الزوايا والخطوط التي رأى أنها صحيحة بشكل بديهي ولا حاجة لتوضيحها.
- يمكن رسم خط مستقيم يصل أي نقطتين في الفراغ، وتسمى بالقطعة المستقيمة.
- يمكن إيجاد قطعة مستقيمة ذات أي طول. (أي أنها قد تمتد إلى ما لانهاية).
- بمعلومية نقطة وقطعة مستقيمة تبدأ من تلك النقطة، يمكن رسم دائرة متمركزة حول تلك النقطة ويساوي نصف قطرها طول القطعة المستقيمة.
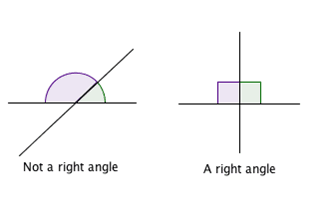
- كل الزوايا القائمة متساوية.
(قد يبدو غريبًا لك الحاجة إلى توضيح ذلك، إذ أن كل الزوايا القائمة قياسها 90 درجة، وبالتالي فهي بالتأكيد متساوية. لكن ذلك لم يكن تعريف إقليدس للزاوية القائمة، إذ لم يكن لديه وسيلة لقياس الزاوية بالدرجات (الزاوية القائمة عند إقليدس هي أي زاوية تنتُج عن تقاطع مستقيمين بحيث يتساوى قياس الزاويتين الناتجتين عن التقاطع).
- عند رسم قطعة مستقيمة بحيث تتقاطع مع مستقيمين، ويكون مجموع قياس الزاويتين الداخليتين الناتجتين من التقاطع أقل من مجموع زاويتين قائمتين، فإن المستقيمين يتقاطعان.
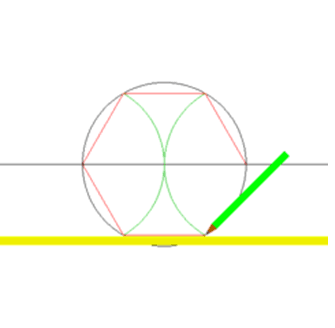
ثمة العديد مما يمكن فعله باستخدام مسلمات إقليدس، كرسم شكل سداسي منتظم.
أو يمكنك تنصيف زاوية. أي قسمها إلى زاويتين متساويتين.
بالفعل تلك هي الأدوات والطرق التي استخدمها العمال لصنع الزينات والنوافذ الجميلة في الكنائس والأديرة.
لكن المسلمة الخامسة من مسلمات إقليدس سببت بعض المشاكل للرياضيين؛ فقد ظنوا أنها يجب أن تتبع كاستنتاج من المسلمات الأربع الأولى. وقد قادت محاولتهم لبرهنة ذلك في النهاية إلى اكتشاف عالم الهندسة اللاإقليدية الغريب والعجيب.
- ترجمة: أحمد اليماني
- تدقيق: حسام التهامي
- تحرير: زيد أبو الرب